Résistance

Résistances axiales pour montage traversant

Résistance CMS pour montage en surface

Définition

La résistance électrique traduit la propriété d’un composant à s’opposer au passage d’un courant électrique (l’une des causes de perte en ligne d’électricité). Elle est souvent désignée par la lettre R et son unité de mesure est l’ohm (symbole : Ω). Elle est liée aux notions de résistivité et de conductivité électrique.
La résistance est responsable d’une dissipation d’énergie sous forme de chaleur. Cette propriété porte le nom d’effet Joule. Cette production de chaleur est parfois un effet souhaité (résistances de chauffage), parfois un effet néfaste (pertes Joule) mais souvent inévitable. (Wikipedia)

Plus la valeur d’une résistance est élevée, plus elle « résiste » au passage du courant. La valeur d’une résistance s’exprime en OHM de symbole  Ω.

Technologie

Ici nous ne nous intéressons qu’aux résistances axiales (celles qui ont 2 fils) utilisables sur les cartes de prototypage.

Carbone aggloméré

La technologie d’origine des résistances axiales est le carbone aggloméré :

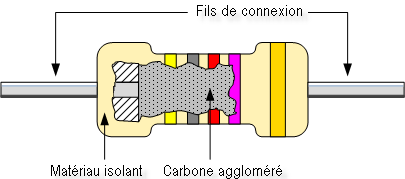
C’est la technologie la plus ancienne. Un cylindre constitué de minuscules grains de carbone est aggloméré sous pression. Un fil est pressé à chaque extrémité du cylindre pour assurer le contact, une couche de résine protège l’ensemble.
Selon la taille des grains, la pression… La valeur de la résistance sera différente. La valeur est indiquée par un code de couleur (voir ci-dessous).
Ces résistances étaient tributaires des aléas de la fabrication, et souvent la valeur de la résistance différait de la valeur inscrite (tolérance 10 à 20%).

Couche de carbone

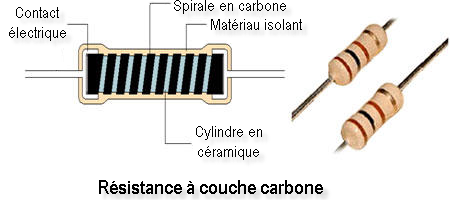
Ce modèle de résistance plus récent est constitué d’un cylindre en céramique sur lequel a été déposé un film de carbone. Ce film est découpé (mécaniquement ou au laser) selon une hélice, ce qui augmente le trajet du courant et donc la résistance. Plus précise, cette résistance à couche carbone offre une tolérance de ± 5%. Elle présente un coefficient de température de ± 300 à 1500 ppm/°C.

Couche métallique

Sur ce modèle de résistance, la couche de carbone est remplacée par une couche métallique. La précision atteint cette fois ± 0,1 à 2% et le coefficient de température ne dépasse pas ± 100 ppm/°C.

Code des couleurs

Les résistances axiales sont repérées par un code de couleur :

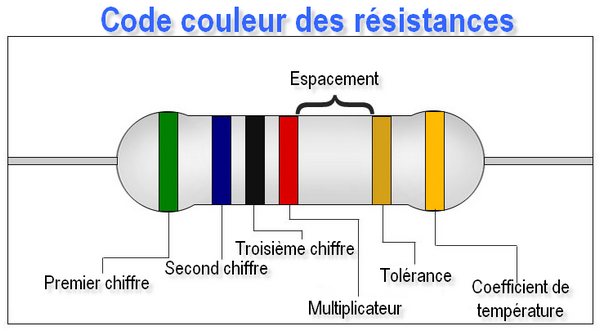Les couleurs correspondent aux valeurs du tableau ci-dessous. En général le troisième chiffre est absent (sauf sur les résistances de précision).

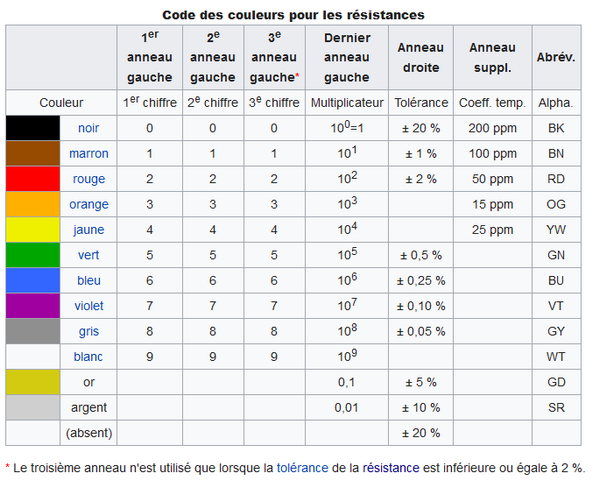Un moyen mnémotechnique pour se souvenir de l’ordre des couleurs dans le code couleur des résistances est de connaitre la phrase suivante :
« Ne Manger Rien Ou Jeûner Voilà Bien Votre Grande Bêtise »
ou encore
« Ne Mangez Rien Ou Je Vous Brûle Votre Grande Barbe« ,
et une dernière phrase
« Ne Mangez Rien Ou Je Vous Bats Violemment Gros Bêta« 
est intéressante car elle permet de repérer la position du violet à travers le mot « Violemment ». Chaque initiale correspond à la première lettre de chaque couleur. (Wikipedia)

Exemple

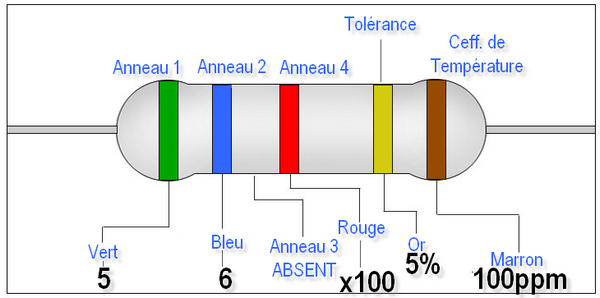Dans cet exemple, le code couleur pour la valeur de la résistance est  Vert  Bleu  Rouge.
Le troisième anneau est absent car c’est une résistance « normale » et pas une résistance de précision. C’est généralement ce type de résistance que vous utiliserez.

• Vert = 5
• Bleu = 6
• Rouge =  x100
  

La résistance vaut donc 5600 Ω  ou encore 5,6 KΩ.

Lot de résistances 5600 Ω

Ci dessus un lot de résistances 5600 Ω. C’est un cas réel. observez bien… Toutes les résistances ne sont pas dans le même sens. Repérez l’anneau vert 🙂 Ce modèle n’a pas d’anneau pour indiquer le coefficient de température. Juste un anneau couleur Or qui indique une précision de ± 5%.
Vous voyez qu’entre la théorie et la réalité, il y a parfois souvent toujours des différences ! Seule l’expérience et un bon appareil de mesure vous mettront à l’abri des erreurs.

Les résistances ont des valeurs normalisées, définies par la norme CEI 60063

[stextbox id=’alert’ caption=’Attention !’]Si, comme moi, vous êtes daltonien, tout ce qui précède ne sert à rien. A vous de trouver comment ranger, étiqueter vos résistances. Pensez aussi à vous munir d’un multimètre pour vérifier les valeurs avant de connecter ces composants ![/stextbox]

Mise en série des résistances

Lorsque vous mettez des résistances en série, leurs valeurs s’ajoutent :

R_tot = R₁ + R₂ +… + R_n

Exemple : si vous mettez en série 3 résistances de 100 Ω la résistance résultante vaudra 300 Ω .

Mise en parallèle des résistances

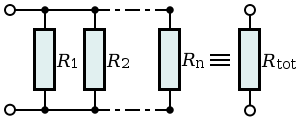
Pour simplifier nous allons prendre des résistances identiques (pour en savoir plus, voyez Wikiversity). Lorsque vous mettez des résistances identiques en parallèle la valeur finale vaut :

R_tot = R / n

Avec R : la valeur de chaque résistance et n le nombre de résistances.

Par exemple si vous mettez 3 résistances de 10 KΩ en parallèle, vous obtenez une résistance de

10 KΩ / 3 = 3300Ω

Les derniers chiffres ont peu d’importance compte tenu de la tolérance sur la valeur de la résistance. J’aurais pu écrire 3333 Ω mais si la résistance a une tolérance de ±5%, elle peut avoir n’importe quelle valeur entre 3499Ω et 3166Ω… donc 3300Ω est une valeur tout à fait acceptable (j’ajoute ça pour les pointilleux).

Si le cas des résistances de valeurs différentes mises en parallèle vous intéresse, consultez ce lien sur Wikipedia.

Utilisation

Les résistances sont utilisées principalement (en ce qui nous concerne) pour

• Diviser une tension
• Limiter le courant dans un composant (LED, transistor etc.)

Voyons rapidement comment ça fonctionne.

Diviser une tension

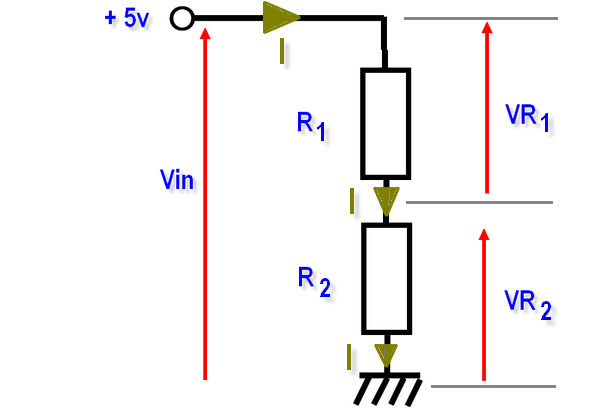
Lorsqu’on applique la tension de 5 volts sur les deux résistances, un courant circule dans les résistances. Ce courant noté I (Intensité) arrive par la borne +5 volts, traverse R1 puis R2 avant de rejoindre la masse. Il est identique en tous endroits du circuit, ce qui permet en appliquant les formules de base de l’électricité de calculer la tension présente aux bornes de chacune des résistances.

Les résistances en série s’ajoutent (voir ici)  R_Totale=R₁+R₂  le courant vaut I=V_in/(R₁+R₂)

On peut donc calculer V_R1= R₁ x I  et  V_R2=R_2 x I. En « tritouillant » les équations on peut s’arranger pour calculer directement la valeur aux bornes d’une des résistances, sans calculer d’abord le courant. On arrive à

Le mieux est de prendre un exemple. La tension d’entrée est de 5 volts, R1 = 1KΩ et R2 = 2KΩ. Quelle est la tension aux bornes de la résistance R2 ?

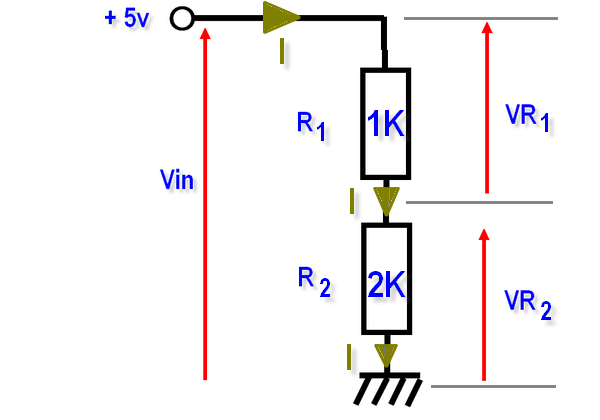
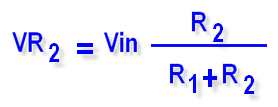
La tension aux bornes de R2 vaut VR2 = 5 x R1/(R1+R2) soit 5 x 2K/(1K+2K) = 5 x (2/3)
On arrive donc à une tension de 10/3 = 3,3 volts aux bornes de R2. Voilà qui est intéressant car un module qui fournit un signal de sortie en 5 volts peut ainsi s’interfacer avec nos GPIO qui n’acceptent pas de tension supérieure à 3,3 volts.

Calculateur de pont diviseur

Pour ceux que les calculs rebutent, je vous offre ce calculateur de tension de sortie pour le pont diviseur. Faites glisser le curseur pour choisir la tension (entre 0 et 24 volts) et saisissez la valeur de R1 et R2 en OHM. La tension de sortie s’affiche directement 🙂

Limiter le courant dans une LED

Nota : Ce paragraphe utilise une LED, composant qui sera vu plus en détail immédiatement à la suite.

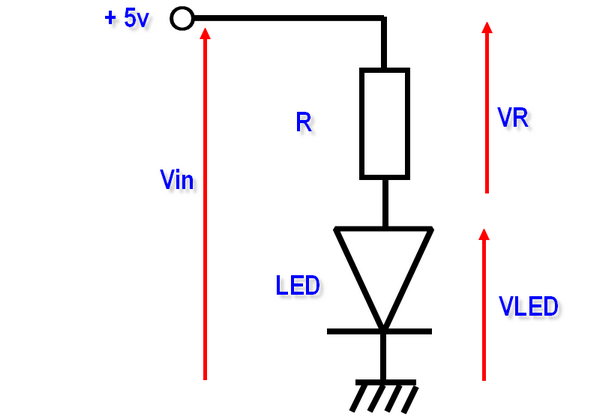Dans cet exemple, la LED rouge est alimentée à partir du 5 Volt. Comme dans le cas du pont diviseur à résistance vu précédemment, le même courant I circule dans la résistance et dans la LED. Du fait des caractéristiques de la diode LED, la tension à ses bornes est fixe et égale à environ 1,6 volts (tension caractéristique d’une LED rouge).

Comme on applique une tension Vin de 5 volts, celle-ci se répartit entre la résistance et la LED.

V_in = V_R + V_LED

On peut en déduire que V_R = V_in – V_LED.

Pour allumer une LED « normale » (c’est quoi normale ?) il faut tabler sur un courant de 10 mA environ (mais ça peut être plus… ou moins, selon la LED). Quelle valeur donner à la résistance R pour que le courant qui parcourt le circuit soit de 10 mA ?

Comme il y a 1,6 volts aux bornes de la diode LED rouge, il reste 5 – 1,6 = 3,4 volts aux bornes de la résistance. Comme j’ai choisi un courant de 10 mA cette résistance parcourue par un courant de 10 mA présente une tension de 3,4 volts à ses bornes…

V_R = R x I

on peut en déduire la valeur de R :          R = V_R/I

avec VR = 3,4 volts et I = 10 mA ce qui donne R = 3,4 / 0,010 = 340 Ω.

Là encore la précision n’est pas de mise. Si vous trouvez une résistance de 300Ω, elle fera l’affaire. Une résistance de 470Ω aussi 😉 simplement dans ce cas la LED éclairera un peu moins. SI vous ne trouvez que 2 résistances de 1KΩ, pas de souci, mettez les en parallèle, vous obtiendrez 500Ω, pas loin de 470Ω, et la LED s’allumera. Si vous avez 3 résistances de 1K, mettez les en parallèle, ça fera une résistance de 330Ω et… ça fonctionnera aussi etc.

Calculateur de résistance pour LED